Математика Проценты содержания (по весу) спирта в трех растворах образуют геометрическую прогрессию

Задача: проценты содержания (по весу) спирта в трех растворах образуют геометрическую прогрессию. Если смешать первый, второй и третий растворы в весовом отношении 2 : 3 : 4, то получится раствор, содержащий 32 % спирта. Если же смешать их в весовом отношении 3 : 2 : 1, то получится раствор, содержащий 22 % спирта. Сколько процентов спирта содержит первый раствор?
Решение:



Ответ: a=12%, b=24%, c=48%
* 5 * 5 * 5 * 5 * 5 *
Удачи тебе на экзаменах! У тебя всё получится - мы в тебя верим!
Поделись этой информацией с помощью кнопок ниже (облегчи учёбу другим ученикам, и будет тебе плюс в карму!)
ТЕОРИЯ. Основные формулы арифметической прогрессии
Рекуррентная формула n-го члена: an+1 = an + dФормула n-го члена: an = a1 + d(n — 1)Сумма первых n членов 1-я формула 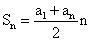 Сумма первых n членов 2-я формула
Сумма первых n членов 2-я формула 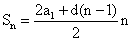 Характеристическое свойство
Характеристическое свойство 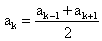 Свойство крайних членов a1 + an = a2 + an-1 = a3 + an-2 = …Основные формулы геометрической прогрессииРекуррентная формула n-го члена: bn+1 = bn qФормула n-го члена: bn = b1 qn-1Сумма первых n членов 1-я формула
Свойство крайних членов a1 + an = a2 + an-1 = a3 + an-2 = …Основные формулы геометрической прогрессииРекуррентная формула n-го члена: bn+1 = bn qФормула n-го члена: bn = b1 qn-1Сумма первых n членов 1-я формула 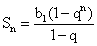 Сумма первых n членов 2-я формула
Сумма первых n членов 2-я формула 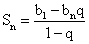 Сумма бесконечной геометрической прогрессии
Сумма бесконечной геометрической прогрессии 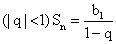 Характеристическое свойство
Характеристическое свойство 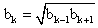 Пример 1.Известно, что 1-й, 7-й и 25 члены арифметической прогрессии с ненулевой разностью составляют геометрическую прогрессию. Найти q.РешениеРассмотрим геометрическую прогрессию, члены которой:
Пример 1.Известно, что 1-й, 7-й и 25 члены арифметической прогрессии с ненулевой разностью составляют геометрическую прогрессию. Найти q.РешениеРассмотрим геометрическую прогрессию, члены которой: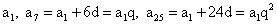
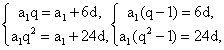 Если разделим второе уравнение на первое, то получим q + 1 = 4, q = 3.Ответ: 3.Пример 2.Три различных числа a, b, c образуют в указанном порядке геометрическую прогрессию. Числа: a + b, b + c, a + c образуют в указанном порядке арифметическую прогрессию. Найти знаменатель геометрической прогрессии.Дано:Г.П.: a1, a1q, a1q2.А.П.: a1 + a1q, a1q + a1q2, a1 + a1q2.Найти q.РешениеВоспользуемся характеристическим свойством арифметической прогрессии:
Если разделим второе уравнение на первое, то получим q + 1 = 4, q = 3.Ответ: 3.Пример 2.Три различных числа a, b, c образуют в указанном порядке геометрическую прогрессию. Числа: a + b, b + c, a + c образуют в указанном порядке арифметическую прогрессию. Найти знаменатель геометрической прогрессии.Дано:Г.П.: a1, a1q, a1q2.А.П.: a1 + a1q, a1q + a1q2, a1 + a1q2.Найти q.РешениеВоспользуемся характеристическим свойством арифметической прогрессии: 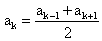
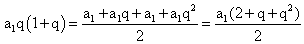
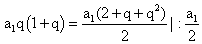 2q + 2q2 — 2 — q — q2 = 0q2 + q — 2 = 0, q = -2, q = 1.Знаменатель геометрической прогрессии не может равняться 1.Ответ: -2.Пример 3.Первый член возрастающей арифметической прогрессии равен 0,2. Найти разность прогрессии, если известно, что при делении каждого ее члена на номер этого члена получается геометрическая прогрессия и число членов прогрессии больше трех.Дано:Г.П.: (0,2 + d)/2; (0,2 + 2d)/3; (0,2 + 3d)/4.Найти d.РешениеВоспользуемся характеристическим свойством геометрической прогрессии:
2q + 2q2 — 2 — q — q2 = 0q2 + q — 2 = 0, q = -2, q = 1.Знаменатель геометрической прогрессии не может равняться 1.Ответ: -2.Пример 3.Первый член возрастающей арифметической прогрессии равен 0,2. Найти разность прогрессии, если известно, что при делении каждого ее члена на номер этого члена получается геометрическая прогрессия и число членов прогрессии больше трех.Дано:Г.П.: (0,2 + d)/2; (0,2 + 2d)/3; (0,2 + 3d)/4.Найти d.РешениеВоспользуемся характеристическим свойством геометрической прогрессии: 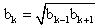
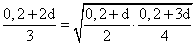 . Возведем обе части в квадрат:1/9(0,22 + 4 0,2d + 4d2) = 1/8(0,22 + 0,2d + 0,6d + 3d2)| 728(0,04 + 0,8d + 4d2) = 9 (0,04 + 0,8d + 3d2)0,32 + 6,4d + 32d2 = 0,36 + 7,2d + 27d25d2 — 0,8d — 0,04 = 0, d = 0,2, d = -0,04.По условию арифметическая прогрессия возрастающая, поэтому разность d > 0.Ответ: 0,2.Пример 4.Три отличных от нуля числа образуют арифметическую прогрессию, а квадраты этих чисел образуют геометрическую прогрессию. Найти все возможные знаменатели последней прогрессии.Дано:А.П.:
. Возведем обе части в квадрат:1/9(0,22 + 4 0,2d + 4d2) = 1/8(0,22 + 0,2d + 0,6d + 3d2)| 728(0,04 + 0,8d + 4d2) = 9 (0,04 + 0,8d + 3d2)0,32 + 6,4d + 32d2 = 0,36 + 7,2d + 27d25d2 — 0,8d — 0,04 = 0, d = 0,2, d = -0,04.По условию арифметическая прогрессия возрастающая, поэтому разность d > 0.Ответ: 0,2.Пример 4.Три отличных от нуля числа образуют арифметическую прогрессию, а квадраты этих чисел образуют геометрическую прогрессию. Найти все возможные знаменатели последней прогрессии.Дано:А.П.: 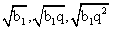 Г.П.:
Г.П.: 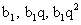 Найти q.РешениеВоспользуемся характеристическим свойством арифметической прогрессии:
Найти q.РешениеВоспользуемся характеристическим свойством арифметической прогрессии: 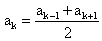
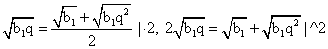
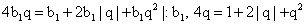
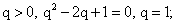
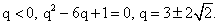 Ответ:
Ответ: 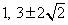 .Пример 5.Цифры трехзначного числа составляют геометрическую прогрессию. Если из данного числа вычесть 297, то получится число, написанное теми же цифрами, но в обратном порядке. Если же к цифрам данного числа, начиная с разряда сотен, прибавлять соответственно 8,5 и 1, то полученные суммы составят арифметическую прогрессию. Найти исходное число.РешениеПусть исходное число
.Пример 5.Цифры трехзначного числа составляют геометрическую прогрессию. Если из данного числа вычесть 297, то получится число, написанное теми же цифрами, но в обратном порядке. Если же к цифрам данного числа, начиная с разряда сотен, прибавлять соответственно 8,5 и 1, то полученные суммы составят арифметическую прогрессию. Найти исходное число.РешениеПусть исходное число 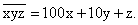 .
.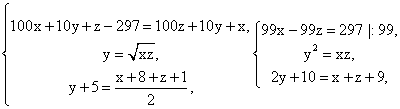
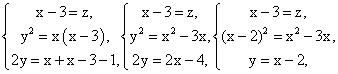 Решим второе уравнение: х2 — 4х + 4 = х2 — 3х, х = 4, тогда у = х — 2 = 2, z = x — 3 = 1.Ответ: 421.Пример 6.Найти четыре числа, из которых первые три составляют геометрическую прогрессию, а последние три составляют арифметическую прогрессию, причем сумма крайних чисел равна 32, а сумма средних чисел равна 24.РешениеПусть x, y, z, t — данные числа.
Решим второе уравнение: х2 — 4х + 4 = х2 — 3х, х = 4, тогда у = х — 2 = 2, z = x — 3 = 1.Ответ: 421.Пример 6.Найти четыре числа, из которых первые три составляют геометрическую прогрессию, а последние три составляют арифметическую прогрессию, причем сумма крайних чисел равна 32, а сумма средних чисел равна 24.РешениеПусть x, y, z, t — данные числа.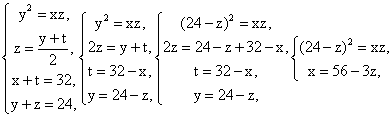 (24 — z)2 = (56 — 3z)z; 576 — 48z + z2 = 56z — 3z2, 4z2 — 104z + 576 = 0,z = 18 или z = 8x = 56 — 3z = 2 или x = 32y = 24 — z = 6 или y = 16t = 32 — x = 30 или t = 0.Ответ: 2, 6, 18, 30 или 32, 16, 8, 0.Пример 7.Сумма первых десяти членов арифметической прогрессии равна 155, а сумма первых двух членов геометрической прогрессии равна 9. Найти эти прогрессии, если первый член арифметической прогрессии равен знаменателю геометрической прогрессии, а первый член геометрической прогрессии равен разности арифметической прогрессии.РешениеЕсли подставим данные задачи в формулы суммы и n-го члена арифметической прогрессии, то получим систему уравнений:
(24 — z)2 = (56 — 3z)z; 576 — 48z + z2 = 56z — 3z2, 4z2 — 104z + 576 = 0,z = 18 или z = 8x = 56 — 3z = 2 или x = 32y = 24 — z = 6 или y = 16t = 32 — x = 30 или t = 0.Ответ: 2, 6, 18, 30 или 32, 16, 8, 0.Пример 7.Сумма первых десяти членов арифметической прогрессии равна 155, а сумма первых двух членов геометрической прогрессии равна 9. Найти эти прогрессии, если первый член арифметической прогрессии равен знаменателю геометрической прогрессии, а первый член геометрической прогрессии равен разности арифметической прогрессии.РешениеЕсли подставим данные задачи в формулы суммы и n-го члена арифметической прогрессии, то получим систему уравнений: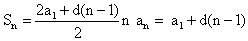
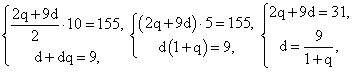 Подставим второе уравнение системы в первое и решим его:
Подставим второе уравнение системы в первое и решим его: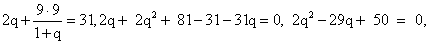 q = 2 или q = 12,5. Тогда d = 3 или d = 2/3.Ответ: 2; 5; 8; … и 3; 6; 12; … или 25/2; 79/6; 83/6; … и 2/3; 25/3; 625/6; …Пример 8.При каком значении параметра a значения функции y = x3 — 6x2 + 9x + a в точке х = 2 и в точках экстремума, взятые в некотором порядке, образуют геометрическую прогрессию?РешениеФункция определена на всей числовой прямой. Достаточно легко найти точки экстремума данной функции:y' = 3x2 — 12x + 9 = 3(x2 — 4x + 3) = 3(x — 1 )(x — 3)y' = 0 при х = 1, х = 3.Найдем значение функции в точках экстремума и в точке х = 2:у(3) = a; у(2) = 2 + a; у(1) = 4 + a.Так как порядок чисел не определен, то необходимо проверить характеристическое свойство геометрической прогрессии, все комбинации:
q = 2 или q = 12,5. Тогда d = 3 или d = 2/3.Ответ: 2; 5; 8; … и 3; 6; 12; … или 25/2; 79/6; 83/6; … и 2/3; 25/3; 625/6; …Пример 8.При каком значении параметра a значения функции y = x3 — 6x2 + 9x + a в точке х = 2 и в точках экстремума, взятые в некотором порядке, образуют геометрическую прогрессию?РешениеФункция определена на всей числовой прямой. Достаточно легко найти точки экстремума данной функции:y' = 3x2 — 12x + 9 = 3(x2 — 4x + 3) = 3(x — 1 )(x — 3)y' = 0 при х = 1, х = 3.Найдем значение функции в точках экстремума и в точке х = 2:у(3) = a; у(2) = 2 + a; у(1) = 4 + a.Так как порядок чисел не определен, то необходимо проверить характеристическое свойство геометрической прогрессии, все комбинации:
- 1) проверим порядок: a; 2 + a; 4 + a: (2 + a)2 = a(4 + a); 4 + 4a + a2 = 4a + a2;4 = 0, неверно;2) проверим порядок: a; 4 + a; 2 + a: (4 + a)2 = a(2 + a); 16 + 8a + a2 = 2a + a2;6a = -16; a = -8/3;3) проверим порядок: 4 + a; a; 2 + a: a2 = (4 + a)(2 + a); a2 = 8 + 6a + a2;6a = -8; a = -4/3.
Ответ: -8/3; -4/3.Пример 9.В трех растворах проценты содержания (по массе) спирта образуют геометрическую прогрессию. Если смешать первый, второй и третий растворы в весовом отношении 2 : 3 : 4, то получится раствор, содержащий 32% спирта. Если же смешать их в весовом отношении 3 : 2 : 1, то получится раствор, содержащий 22% спирта. Сколько процентов спирта содержит каждый раствор?РешениеПусть p1, р2, р3 — концентрации данных растворов. По условию р2 = p1q, p3 = р1q2, где q — знаменатель прогрессии. Используя формулу:m1p1 + m2p2 + m3p3 = p(m1 + m2 + m3), составим систему уравнений: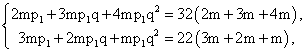 Разделим все уравнения на m > 0.56-030.gifЧтобы избавиться от третьего слагаемого, содержащего вторую степень, умножим второе уравнение на (-4 ) и сложим его с первым уравнением:
Разделим все уравнения на m > 0.56-030.gifЧтобы избавиться от третьего слагаемого, содержащего вторую степень, умножим второе уравнение на (-4 ) и сложим его с первым уравнением: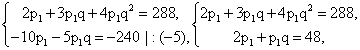
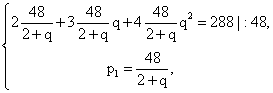 Решим первое уравнение:
Решим первое уравнение: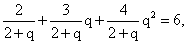 2 + 3q + 4q2 = 12 + 6q, 4q2 — 3q — 10 = 0, q = -1,25 или q = 2. Отрицательный корень не удовлетворяет условию задачи.Итак, р1 = 48/(2 + 2) = 12%, р2 = p1q = 12 2 = 24%, p3 = р1q2 = 12 22 = 48%.Ответ: 12, 24, 48.Пример 10.Три конькобежца, скорости которых в некотором порядке образуют геометрическую прогрессию, одновременно стартуют (из одного места) по кругу. Через некоторое время второй конькобежец обгоняет первого, пробежав на 400 м больше его. Третий конькобежец пробегает то расстояние, которое пробежал первый к моменту обгона его вторым, за время на 2/3 минуты больше, чем первый. Найти скорость первого конькобежца.РешениеНетрудно догадаться, что самый «быстрый» из конькобежцев — это второй, на втором месте — первый, и самый «медленный» — третий. Поэтому пусть скорости конькобежцев в возрастающем порядке:v3 = v, v1 = vq, v2 = vq2.
2 + 3q + 4q2 = 12 + 6q, 4q2 — 3q — 10 = 0, q = -1,25 или q = 2. Отрицательный корень не удовлетворяет условию задачи.Итак, р1 = 48/(2 + 2) = 12%, р2 = p1q = 12 2 = 24%, p3 = р1q2 = 12 22 = 48%.Ответ: 12, 24, 48.Пример 10.Три конькобежца, скорости которых в некотором порядке образуют геометрическую прогрессию, одновременно стартуют (из одного места) по кругу. Через некоторое время второй конькобежец обгоняет первого, пробежав на 400 м больше его. Третий конькобежец пробегает то расстояние, которое пробежал первый к моменту обгона его вторым, за время на 2/3 минуты больше, чем первый. Найти скорость первого конькобежца.РешениеНетрудно догадаться, что самый «быстрый» из конькобежцев — это второй, на втором месте — первый, и самый «медленный» — третий. Поэтому пусть скорости конькобежцев в возрастающем порядке:v3 = v, v1 = vq, v2 = vq2.
| S | v | t | |
| I | S | vq | t |
| I I | S + 400 | vq2 | t |
| I I I | S | v | t + 2 / 3 |
- Используя первые две строки таблицы, найдем S из системы:
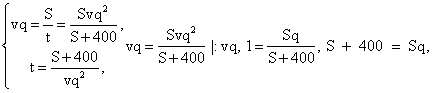 S(q — 1) = 400, S = 400 / (q - 1).
S(q — 1) = 400, S = 400 / (q - 1). - Используя первую и третью строки таблицы, найдем t из системы:
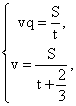 Разделим первое уравнение на второе, получим:
Разделим первое уравнение на второе, получим: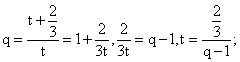
- Найдем скорость первого конькобежца:
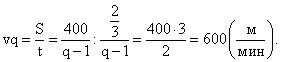
Ответ: 600.
Теоретические сведения и примеры
Рассмотрим множество натуральных чисел N. Каждому натуральному числу по определенному правилу поставим в соответствие некоторое другое число. Получим бесконечную числовую последовательность, которую можно считать функцией, заданной на множестве натуральных чисел. Числовую последовательность принято обозначать  или аn, где
или аn, где  Последовательность чаще всего задается формулой n-го члена или дается правило, по которому, зная предыдущие члены, можно вычислить последующие (рекуррентное задание последовательности).
Последовательность чаще всего задается формулой n-го члена или дается правило, по которому, зная предыдущие члены, можно вычислить последующие (рекуррентное задание последовательности).
Например, последовательность чисел 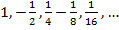
может быть задана формулой 
Действительно, если  то
то  , если
, если  , то
, то  и т. д.
и т. д.
Числовая последовательность может быть конечной, если в ней содержится ограниченное количество чисел, т. е. сопоставление проводится не для всех натуральных чисел, а только для некоторых из них.
Если каждый член последовательности, начиная со второго, больше предыдущего, то последовательность называется монотонно возрастающей. Если каждый член последовательности, начиная со второго, меньше предыдущего, то последовательность называется монотонно убывающей. Монотонно возрастающие и монотонно убывающие последовательности иногда называются просто монотонными.
Особый интерес для нас представляют последовательности, называемые арифметической и геометрической прогрессиями.
Числовая последовательность называется арифметической прогрессией, если каждый ее член, начиная со второго, равен предыдущему, сложенному с одним и тем же числом, т. е. арифметическая прогрессия задается рекуррентно следующим образом:  где
где  (число d называется разностью прогрессии). Зная первый член прогрессии, а также ее разность, можно вычислить значение любого другого члена прогрессии:
(число d называется разностью прогрессии). Зная первый член прогрессии, а также ее разность, можно вычислить значение любого другого члена прогрессии: 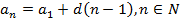 .
.
Каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому соседних с ним членов, т. е.  где
где  характеристическое свойство арифметической прогрессии.
характеристическое свойство арифметической прогрессии.
Формула суммы первых n членов прогрессии:
 или
или  ,
,  .
.
Если разность арифметической прогрессии – положительное число, то такая прогрессия называется возрастающей; если разностью является отрицательное число, то прогрессия называется убывающей.
Из определения разности арифметической прогрессии
 следует, что
следует, что  т. е. сумма членов, равноудаленных от концов прогрессии, есть величина постоянная.
т. е. сумма членов, равноудаленных от концов прогрессии, есть величина постоянная.
Числовая последовательность называется геометрической прогрессией, если первый ее член отличен от нуля, а каждый последующий равен предыдущему, умноженному на некоторое постоянное для данной последовательности число, отличное от нуля. Геометрическая прогрессия задается рекуррентно следующим образом: 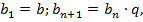 где
где  (число q называется знаменателем прогрессии).
(число q называется знаменателем прогрессии).
Для того чтобы задать геометрическую прогрессию, достаточно знать ее первый член и знаменатель, тогда всякий член прогрессии может быть вычислен по формуле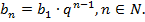
Из определения геометрической прогрессии следует, что отношение любого ее члена к предшествующему равно одному и тому же числу, т. е. 
Если  то все члены прогрессии равны между собой. В этом случае прогрессия является постоянной последовательностью. Если
то все члены прогрессии равны между собой. В этом случае прогрессия является постоянной последовательностью. Если  то прогрессия является монотонной последовательностью, а именно возрастающей, если
то прогрессия является монотонной последовательностью, а именно возрастающей, если 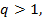 и убывающей, если
и убывающей, если  Если
Если  то прогрессия называется возрастающей по абсолютной величине, если же
то прогрессия называется возрастающей по абсолютной величине, если же  то прогрессия называется убывающей по модулю. В случае, когда число членов убывающей прогрессии бесконечно, прогрессия называется бесконечно убывающей.
то прогрессия называется убывающей по модулю. В случае, когда число членов убывающей прогрессии бесконечно, прогрессия называется бесконечно убывающей.
Прогрессия называется геометрической тогда и только тогда, когда каждый ее член, начиная со второго, равен среднему геометрическому соседних с ним членов, т. е.  где
где  (характеристическое свойство геометрической прогрессии).
(характеристическое свойство геометрической прогрессии).
Формула суммы первых n членов прогрессии  или
или  (в случае
(в случае 
 ).
).
Если геометрическая прогрессия, бесконечно убывающая  то ее сумма вычисляется по формуле
то ее сумма вычисляется по формуле 
Задача 1.Сумма трех положительных членов арифметической прогрессии равна 21. Если к этим числам прибавить 2; 3 и 9 соответственно, то новые числа образуют геометрическую прогрессию. Найти эти числа.
Решение. Пусть  – первые члены арифметической прогрессии и их сумма равна 21, т. е.
– первые члены арифметической прогрессии и их сумма равна 21, т. е. 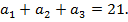 Так как прогрессия арифметическая, то
Так как прогрессия арифметическая, то 
По условию задачи числа  образуют геометрическую прогрессию, т.е
образуют геометрическую прогрессию, т.е  .
.
Получим систему уравнений и решим ее:





Уравнение  имеет один целый положительный корень
имеет один целый положительный корень 
Отсюда  Значит, числа 5; 10; 20 образуют геометрическую прогрессию.
Значит, числа 5; 10; 20 образуют геометрическую прогрессию.
Ответ: искомые числа 5; 10; 20.
Задача 2. Найти сумму первых четырех членов геометрической прогрессии, обладающей тем свойством, что ее первые три члена, сумма которых равна  являются одновременно первым, четвертым и восьмым членами некоторой арифметической прогрессии.
являются одновременно первым, четвертым и восьмым членами некоторой арифметической прогрессии.
Решение. Пусть числа  образуют геометрическую прогрессию, причем
образуют геометрическую прогрессию, причем  Так как
Так как  является одновременно первым,
является одновременно первым,  – четвертым членами некоторой арифметической прогрессии, то
– четвертым членами некоторой арифметической прогрессии, то  , где d – разность этой арифметической прогрессии. Но
, где d – разность этой арифметической прогрессии. Но  является также восьмым членом этой же прогрессии, поэтому
является также восьмым членом этой же прогрессии, поэтому 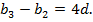 Данные условия можно записать в виде системы уравнений
Данные условия можно записать в виде системы уравнений 
Разделив второе уравнение на первое, получим  Но
Но  отсюда
отсюда  Найдем сумму первых четырех членов геометрической прогрессии по формуле:
Найдем сумму первых четырех членов геометрической прогрессии по формуле:

Ответ: сумма первых четырех членов 
Задача 3. В трех растворах проценты содержания спирта образуют геометрическую прогрессию. Если смешать первый, второй и третий растворы в весовом отношении 2:3:4, то получится раствор, содержащий 32 % спирта. Если же смешать их в весовом отношении 3:2:1, то получится раствор, содержащий 22 % спирта. Каков процент спирта в каждом растворе?
Решение. Пусть х – концентрация спирта в первом растворе. Так как проценты содержания спирта в трех растворах образуют геометрическую прогрессию, то 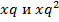 – концентрации спирта во втором и третьем растворах соответственно (q – некоторое постоянное число). Если взять две части первого раствора, три части второго и четыре части третьего, то получится 9 частей 32%-го раствора спирта, т. е.
– концентрации спирта во втором и третьем растворах соответственно (q – некоторое постоянное число). Если взять две части первого раствора, три части второго и четыре части третьего, то получится 9 частей 32%-го раствора спирта, т. е.  Для второго случая уравнение имеет вид
Для второго случая уравнение имеет вид 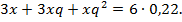
Решим систему уравнений:


Исключим х из уравнений:  или
или 
Получим уравнение  которое имеет один положительный корень
которое имеет один положительный корень  . При
. При  Значит, растворы содержат 12; 24 и 48 % спирта соответственно.
Значит, растворы содержат 12; 24 и 48 % спирта соответственно.
Ответ: первый раствор содержит 12 % спирта, второй – 24 %, третий – 48 %.
Задача 4.
Решить уравнение 
Решение. Перепишем уравнение в виде  Отсюда
Отсюда 
Левая часть уравнения представляет собой арифметическую прогрессию, первый член которой равен 2 и разность равна 2. Число членов прогрессии равно х.
Найдем сумму этой прогрессии.

Из предыдущего равенства  .
.
Полученное уравнение 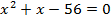 имеет один положительный корень
имеет один положительный корень  который является решением исходного уравнения.
который является решением исходного уравнения.
Ответ: 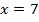 .
.
Задача 5. Решить уравнение :

Решение. Допустимые значения неизвестного удовлетворяют условию
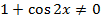 или
или 
В числителе и знаменателе дроби – геометрические бесконечно убывающие прогрессии, суммы которых равны, согласно формуле, соответственно 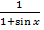 и
и  .
.
Исходное уравнение примет вид

 ⇒
⇒



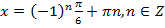
Ответ: 
Решение задач на смеси и сплавы с помощью схем и таблиц
Задачи на смеси и сплавы вызывают наибольшие затруднения у школьников. В процессе решения каждой такой задачи целесообразно действовать по следующей схеме.
1. Изучение условия задачи. Выбор неизвестных величин (их обозначаем буквами х, у и т.д.), относительно которых составляем пропорции. Выбирая неизвестные параметры, мы создаем математическую модель ситуации, описанной в условии задачи.
2. Поиск плана решения. Используя условия задачи, определяем все взаимосвязи между данными величинами.
3. Осуществление плана, т.е. оформление найденного решения – переход от словесной формулировки к составлению математической модели.
4. Изучение полученного решения, критический анализ результата.
При решении задач на смеси часто путают проценты и доли, раствор и растворенное вещество. Необходимо помнить, что массовая доля ![]() находится делением значения процентной концентрации на 100%, а масса растворенного вещества m(в-ва) равна произведению массы раствора m(р-ра) на массовую долю:
находится делением значения процентной концентрации на 100%, а масса растворенного вещества m(в-ва) равна произведению массы раствора m(р-ра) на массовую долю:
m(в-ва) = m(р-ра)•![]() .
.
В большинстве случаев задачи на смеси и сплавы становятся нагляднее, если при их решении использовать схемы, иллюстративные рисунки или вспомогательные таблицы.
Задача 1. В каких пропорциях нужно смешать а%-й и b%-й растворы кислоты (a < b), чтобы получить с%-й раствор?
Возьмем х г а%-го раствора и у г b%-го раствора кислоты. Составим таблицу:
| Kонцентрация раствора, % | Масса раствора, г | Масса кислоты, г |
|---|---|---|
| a | х | 0,01ax |
| b | у | 0,01by |
| c (смесь) | x + y | 0,01c(x + y) |
(b – с)у = (с – а)х,
x : у = (b – с) : (с – а).
Воспользуемся диагональной схемой*:
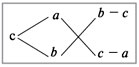
В этой схеме а и b – концентрации исходных растворов, с – требуемая концентрация кислоты в процентах, а «крест-накрест» – записаны их разности (b – с) и (с – а), соответствующие отношению масс растворов а и b.
Задача 2. Сколько по массе 90%-го и 60%-го растворов фосфорной кислоты надо взять, чтобы получить 5,4 кг 80%-го раствора фосфорной кислоты?
Решение
Составим диагональную схему:
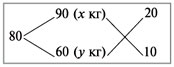
Получаем:
х : у = 20 : 10 = 2 : 1.
Значит, 90%-го раствора фосфорной кислоты надо взять в 2 раза больше, чем 60%-го, т.е. х = 2y.
Составим уравнение: 2y + y = 5,4.
Отсюда y = 1,8 кг.
Ответ. 3,6 кг 90%-го и 1,8 кг 60%-го
растворов фосфорной кислоты.
Задача 3. Сплавили два слитка серебра: 75 г 600-й и 150 г 864-й пробы. Определить пробу сплава.
Решение
Пусть проба сплава равна х.
Составим диагональную схему:
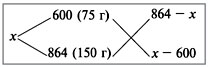
Получаем:
(864 – х) : (х – 600) = 75 : 150 = 1 : 2;
1728 – 2х = х – 600; х = 776.
Ответ. Получили сплав 776-й пробы.
Задача 4. Смешали некоторые количества 72%-го и 58%-го растворов кислоты, в результате получили 62%-й раствор той же кислоты. Если бы каждого раствора было взято на 15 л больше, то получился бы 63,25%-й раствор. Сколько литров каждого раствора было взято первоначально для составления первой смеси?
Решение
Дважды используем диагональную схему:
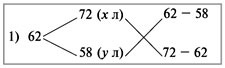
Получаем:
х : у = 4 : 10 = 2 : 5.
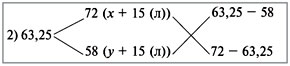
Получаем:
(х + 15) : (y + 15) = 5,25 : 8,75 = 3 : 5.
Составим систему уравнений и решим ее:
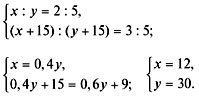
Ответ. В первой смеси было 12 л 72%-го раствора
и 30 л 58%-го раствора.
Задача 5. Сколько граммов 9%-го раствора спирта можно получить из 200 г 70%-го раствора спирта?
Решение
9%-й раствор спирта получают из 70%-го, разбавляя его водой. В воде 0% спирта. Применим диагональную схему:
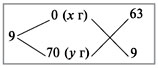
Получаем:
х : у = 63 : 9 = 7 : 1.
Значит, 1 часть 70%-го раствора спирта надо разбавить 7 частями воды. Поэтому 200 г 70%-го раствора спирта надо разбавить 200•7 = 1400 г воды.
Всего получим: 200 + 1400 = 1600 г 9%-го раствора спирта.
Ответ. Из 200 г 70%-го раствора спирта можно
получить 1 кг 600 г 9%-го раствора спирта.
Задача 6. Имеются три смеси (I–III), составленные из трех элементов А, В и С. В первую смесь входят только элементы А и В в массовом отношении 1 : 2, во вторую смесь входят только элементы В и С в массовом отношении 1 : 3, в третью смесь входят только элементы А и С в массовом отношении 2 : 1. В каком соотношении нужно взять эти смеси, чтобы во вновь полученной смеси элементы А, В и С содержались в массовом отношении 11 : 3 : 8?
Решение
Для решения задачи составим схему 1:
Схема 1
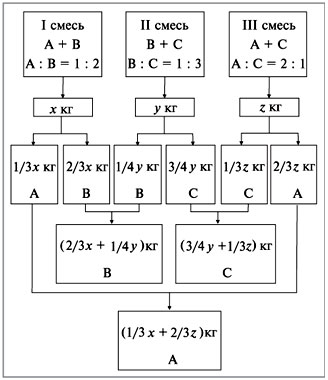
По условию задачи в полученной смеси соотношение масс А : В : С = 11 : 3 : 8. Поэтому
![]()
Составим систему уравнений и решим ее:
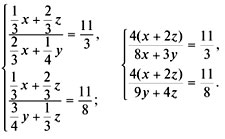
Пусть ![]() = а,
= а, ![]() = b, тогда система примет вид:
= b, тогда система примет вид:
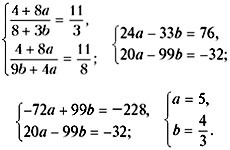
Значит,
х : z = 1 : 5 = 3 : 15, х : у = 3 : 4,
поэтому
х : у : z = 3 : 4 : 15.
Ответ. Чтобы элементы А, В и С содержались
в массовом отношении 11 : 3 : 8, смеси I, II, III
надо взять в соотношении 3 : 4 : 15 по массе.
Задача 7. Имеется два сплава меди, никеля и железа, причем первый из них содержит 4% меди. Если сплавить их в равных количествах, получится сплав, содержащий 66% железа, а если взять 3 кг первого сплава и 7 кг второго, получится сплав, содержащий 0,4 кг меди. Определить процентное содержание никеля во втором сплаве, если известно, что оно в 2 раза выше, чем в первом сплаве.
Решение
Пусть во втором сплаве массовая доля никеля равна x, а железа – у. Для решения задачи составим схему 2.
Исходя из схемы 2, составим и решим систему уравнений:
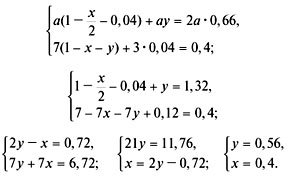
Схема 2
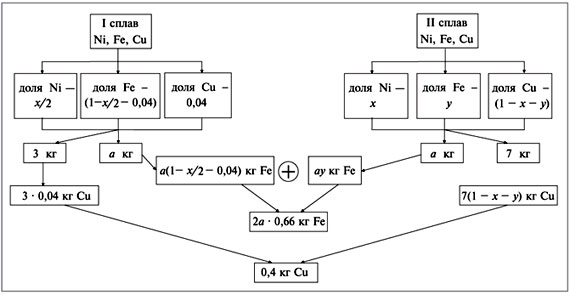
Во втором сплаве массовая доля никеля равна 0,4, т.е. 40%.
Ответ. 40%.
Задача 8. Значения процентного содержания (по объему) спирта в трех растворах образуют геометрическую прогрессию. Если смешать первый, второй и третий растворы в объемном отношении 2 : 3 : 4, то получится 32%-й раствор спирта. Если смешать их в объемном отношении
3 : 2 : 1, то получится раствор, содержащий 22% спирта. Сколько процентов спирта содержит каждый раствор?
Решение
Пусть в первом растворе х% спирта, во втором – у%, в третьем – z%. Согласно условию задачи процентное содержание спирта в трех растворах образует геометрическую прогрессию, потому справедливо уравнение:
у2 = xz. (1)
На основании данных задачи составим таблицы и математические выражения.
Таблица 1
Смешивание трех растворов в объемном отношении 2 : 3 : 4
| Вид раствора | Объем раствора, л | Содержание спирта, % | Объем спирта, л |
|---|---|---|---|
| 1-й раствор | 2 | х | 2х/100 |
| 2-й раствор | 3 | y | 3y/100 |
| 3-й раствор | 4 | z | 4z/100 |
| Cмесь | 9 | 32 | 9•32/100 |
Таблица 2
Смешивание трех растворов в объемном отношении 3 : 2 : 1
| Вид раствора | Объем раствора, л | Содержание спирта, % | Объем спирта, л |
|---|---|---|---|
| 1-й раствор | 3 | х | 3х/100 |
| 2-й раствор | 2 | y | 2y/100 |
| 3-й раствор | 1 | z | z/100 |
| Cмесь | 6 | 22 | 6•22/100 |
3х/100 + 2y/100 + z/100 = 132/100,
3х + 2y + z = 132. (3)
Составим и решим систему из трех уравнений (1–3):
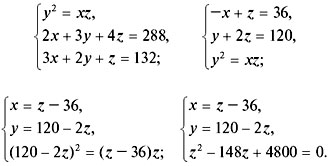
При z1 = 48, x = 12, y = 24;
при z2 = 100, x = 64, y = –80, решение не имеет смысла.
Ответ. В первом растворе 12% спирта,
во втором – 24%, в третьем – 48%.
* При решении задач на смешивание растворов разных концентраций автор использует диагональные схемы («правило креста»). На диагональной схеме в точке пересечения двух прямых обозначают концентрацию смеси. Например, далее в задаче 2 – это 80%. У концов этих прямых слева от точки пересечения указывают концентрации составных частей смеси, а справа – разности концентраций смеси и ее составных частей:
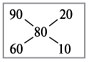
Из этой схемы следует, что, например, для приготовления 30 г 80%-го раствора H3PO4 требуется взять 20 г 90%-го и 10 г 60%-го растворов кислоты.
Облегчи жизнь другим ученикам - поделись! (плюс тебе в карму):



